मला सुचलेले

I am waiting for Inspiration

Posted on November 01, 2025

will update when inspiration strikes

Weight or mass: what we actually measure

Posted on November 01, 2025

Imagine this: You're at your neighbourhood kirana store in Mumbai, haggling over a kilo of atta for your family's Sunday parathas. The shopkeeper slings the bag onto his rusty spring balance, and it dings at "1 kg." You pay up, happy with the deal. But what if that balance was secretly fooling you? What if it wasn't measuring the atta's mass at all, but something else entirely? Welcome to the world of physics where "weight" and "mass" aren't the same – and getting them mixed up could cost you big, even on the Moon. As India's space dreams soar with ISRO's Chandrayaan missions, understanding this is more than school science; it's a superpower for curious minds.

Let's start with the basics. Mass is the amount of "stuff" in an object – think of it as how many atoms are crammed into your cricket bat or that pressure cooker full of dal. It's measured in kilograms (kg) and doesn't change, whether you're in Delhi's humid heat or floating in zero gravity. Mass is stubborn; it's the object's inherent heft, resisting changes in motion (that's inertia, straight out of Newton's laws).

Weight, on the other hand, is the force of gravity pulling that mass down. It's calculated as weight = mass × g, where g is gravity's acceleration – about 9.8 m/s² on Earth. Weight is measured in newtons (N), the unit of force. So, your 5 kg school bag has a mass of 5 kg, but weighs around 49 N on Earth. In everyday Indian lingo, we say "I weigh 50 kg," but technically, that's mass – weight would be the force squishing your bathroom scale.

This mix-up shines brightest with the spring balance, that trusty tool hanging in every dukaan from Kolkata to Kochi. It works like this: Hang your mangoes on the hook, and gravity pulls them down, stretching a coiled spring inside. The stretch is proportional to the force (Hooke's Law: F = k × x, where k is the spring's stiffness and x is the extension). The scale reads that force as "weight." But here's the trick: Most are calibrated to show kilograms, assuming Earth's g. A "1 kg" reading really means "the force of 1 kg under standard gravity" – about 9.8 N. It's handy for labs or markets, but it counters gravity with an equal force from the spring, not directly tallying mass.

A Common Mix-Up: What Happens When You Weigh the Same Object?

Don't get tangled here – a frequent confusion is thinking a 50 kg object on a spring balance would read as 5 kg on a pan balance. Nope, it's the reverse! On Earth, both read 50 kg correctly. But on the Moon (with g ~1/6th of Earth's), the pan balance (a two-pan scale) still reads the true 50 kg, since it compares masses directly – gravity pulls equally on both sides and cancels out. The spring balance, however? It under-reads: that 50 kg object pulls with only 1/6th the force, so the spring stretches less and shows ~8.3 kg. Flip it: To make the spring read "50 kg" on the Moon, you'd need to load ~300 kg of actual mass. The pan balance would then confirm it's truly 300 kg. This mismatch highlights why spring scales fool us in low-gravity spots.

The Moon Scenario - Spring balance made for Earth used on Moon

Now, what if gravity isn't standard? Enter the Moon scenario, a nod to our lunar explorations. Moon's g is just 1/6th of Earth's – about 1.6 m/s². If you're an enterprising teen selling idlis on the Moon (why not? Lunar tourism is coming!), using an Earth-calibrated spring balance spells disaster. Buyer asks for "1 kg of rice flour." To hit the scale's "1 kg" mark, you'd load six times more actual mass, since each kg pulls with only 1/6th the force. You hand over 6 kg for the price of 1 kg – revenue ₹100, but your wholesale cost? ₹600. Boom: ₹500 loss per sale! You'd be out of business faster than a failed Diwali firecracker.

This isn't sci-fi; it's why astronauts train with the mass-weight divide. To measure true mass – independent of gravity – forget springs. Use a two-pan balance scale, like the old brass tare scales in gold souks. It compares your unknown mass against known weights on opposite pans. Gravity pulls equally on both sides, so it cancels out (g divides away in the equation). Equilibrium means equal masses, period. No g drama.

Beyond Earth: Measuring Mass in Space

For zero-gravity spots (hello, future Gaganyaan missions), try an inertial balance (More on this in the next article). It spins the object in a cradle, measuring oscillation time based on inertia alone – mass resists acceleration, gravity be damned. In Indian schools, CBSE physics labs often demo this with simple setups, proving mass is universal.

Why It Matters

So, why care? In a world of ISRO's rocket precision and everyday bazaar bargaining, confusing the two leads to errors – from underdosed medicines to botched space cargo. Next time you weigh veggies, ask: Is this force or fact? It sharpens your mind for engineering entrances like JEE or just smarter shopping.

Picture this finale: On Earth, your spring balance works fine for parathas. But as India eyes Mars, remember – mass is your constant companion; weight is just gravity's fleeting tug. Experiment at home: Weigh a book on a kitchen scale, then "feel" its mass by pushing it. The difference? Pure physics magic. Stay curious, India – the stars (and scales) await.

Bridging the Cosmic Void: Why Understanding Astronomical Instruments is Key to Unlocking the Universe

Posted on October 26, 2025

Think about looking up at the night sky. The stars and galaxies we see are so far away – some light from them has taken millions or even billions of years to reach us. It's like getting a postcard from the start of time! But our eyes alone can't catch all that. That's where special tools, or what we call instruments in astronomy, come in. They act like a strong bridge, helping us cross that huge distance in space. Without them, all that old light would just pass by unnoticed.

For people who study stars – astronomers – these tools are super important. Especially when they sit down to look at the data, like pictures or measurements from the sky. You see, the data doesn't come clean; it's shaped by the tool that caught it. If you don't know how the tool works, what it can pick up and what it misses, then checking the data is like walking in the dark with no torch. No sense in that, right? You might think you see something big, but it could be just a trick from the tool.

Let's talk about these tools a bit. The main one is the telescope. There are different kinds – ones that catch visible light like our eyes do, others for radio waves or heat from far places. For example, the James Webb Space Telescope, or JWST as we call it, is up in space and can see in infrared light. That's heat light, which helps spot baby stars hidden in clouds of dust. Or take the Hubble Telescope – it has cameras that zoom in on colours we can't see from Earth because of our air getting in the way.

But every tool has its own way of working, and limits too. Ground telescopes fight with wind and city lights. Space ones deal with cold or heat from the sun. When data comes in, it's full of these marks – like spots from bad pixels or extra noise. An astronomer must know all this to clean it up. Say you're looking at light from a far galaxy split into colours, like a rainbow. That tells you what's inside it, like gases or stars. But if your tool isn't good at blue colours, you might miss important clues and get the wrong idea about how old the galaxy is.

I remember reading about a funny mistake with Hubble at first. Its mirror was a tiny bit wrong, so stars looked like fuzzy balls, not sharp dots. They fixed it, but only after understanding the tool better. Now, with new tools like JWST's heat camera, you have to watch for warmth from the telescope itself, messing up the view. It's like cooking biryani and making sure the pot doesn't add its own taste!

Today, astronomers use computer programs, like one called Astropy, to test how tools affect data. It helps ask "what if" questions. But you still need to learn the basics first. As I heard a veteran astronomer quip at an astronomy institute, 'Data analysis without understanding the instrument fully is like doing a surgery with oven mitts—messy and misguided.'

Why care about this? Because these tools let us find amazing things: planets that might have life, or waves from black holes crashing. It changes how we see our world and ourselves. For young students, hobby watchers, or anyone curious – start simple. Read about your local telescope, try apps that show star data. Understand the tool, and the sky opens up.

In the end, astronomy is not just collecting info; it's making sense of it with smart eyes. Don't guess – learn the bridge, and step across to the stars. The universe is waiting, simple and wonderful.

Exploring the Venturi Effect: A Journey into Fluid Dynamics

Posted on October 10, 2025

During my science journey, I once pondered the significance of concepts like the Venturi effect. But as fate would have it, my introduction to this idea opened doors to a captivating world of fluid dynamics.

Fertigation, an agricultural method, marked my first encounter with the Venturi effect. Previously, I only associated it with pump sprays. However, seeing it in action, seamlessly injecting water-soluble fertilisers into the main water pipe during fertigation made me realise its practical utility in solving real-world problems.

Named after Giovanni Battista Venturi, an 18th-century scientist, the Venturi effect quietly influences various aspects of our lives. From carburettors in engines to gas burners and musical instruments like the trombone, it's a fundamental principle subtly woven into everyday applications.

Beyond its practical applications, the Venturi effect offers a simple way to understand fluid dynamics. Blowing air between closely spaced surfaces visually illustrates how fluid velocity changes, making the concept more accessible.

My encounter with the Venturi effect changed my perspective on science and math. It's not just about memorising formulas; it's about understanding the world and finding solutions to real problems. The Venturi effect, once mysterious, is now a valuable tool for problem-solving.

So, for my fellow learners, if you ever doubt the relevance of your studies, remember that you're unlocking the secrets of a fascinating universe. Stay curious, keep exploring, and embrace the wonder of the Venturi effect—it may just lead you on an exciting journey of discovery!

The Expanding Universe — Our Endless Journey

Posted on July 10, 2025

Galaxy distances unlocked, Edwin Hubble peered deeper in the 1920s from California's Mount Wilson. Born in 1889, this Missouri farm boy-turned-basketball star ditched law for stars, wielding the world's biggest telescope. He classified "nebulae" as distant galaxies, then measured their speeds via spectra—rainbow fingerprints of light. What he found? Mind-blowing: All but neighbors recede, and faster ones are farther. The universe isn't static—it's ballooning!

Hubble’s Law

Key clue: Redshift. Approaching objects blueshift (wavelengths squeeze); receding ones redshift (stretch to red end), like a siren's wail dropping as it zooms away. Hubble clocked redshifts for 18 galaxies using Leavitt's Cepheids. Plot distance vs. speed: Straight line! Hubble's Law: Velocity = Hubble Constant (H0) x Distance. H0 ≈70 km/s/Mpc means for every megaparsec (3 million light-years) farther, galaxies flee 70 km/s faster. Implication? Space itself expands, carrying galaxies like raisins in rising dough—no center, everything stretches uniformly.

Hubble's 1929 paper sparked the Big Bang theory (coined mockingly by Fred Hoyle in 1949). Georges Lemaître, a Belgian priest-physicist, predicted it in 1927—now it's Hubble-Lemaître Law. Fun fact: Hubble smoked cigars atop his scope; one 1930s photo shows ash nearly scorching a priceless photo plate!

Modern Mapping

Today, Sloan Digital Sky Survey (SDSS) scans one-third the sky with a New Mexico telescope, cataloging 500 million objects since 2000. It maps the "cosmic web": Filaments of galaxies threading voids, like a 3D spiderweb of dark matter and gas, spanning 93 billion light-years observable. SDSS revealed galaxy evolution—early universe was clumpier. But tension brews: Different methods give H0 as 67 or 74 km/s/Mpc, hinting new physics like evolving dark energy.

The Mystery Lives On

Gravitational waves from merging black holes now act as "standard sirens," rippling spacetime to measure distances sans light. Will it solve the Hubble Tension? Maybe you will—future scopes like Euclid hunt the web's secrets. The universe expands at 70 km/s per Mpc, born 13.8 billion years ago, still growing. We're on a cosmic road trip, and the road's lengthening!

Activity: The Balloon Universe

1. Inflate a balloon slightly; dot "galaxies" with marker, measure distances.
2. Blow more; all dots recede, farther ones fastest—no center!
3. Draw "light waves" stretching between dots (redshift).
4. Calculate "H0": Speed/distance ratio stays constant.

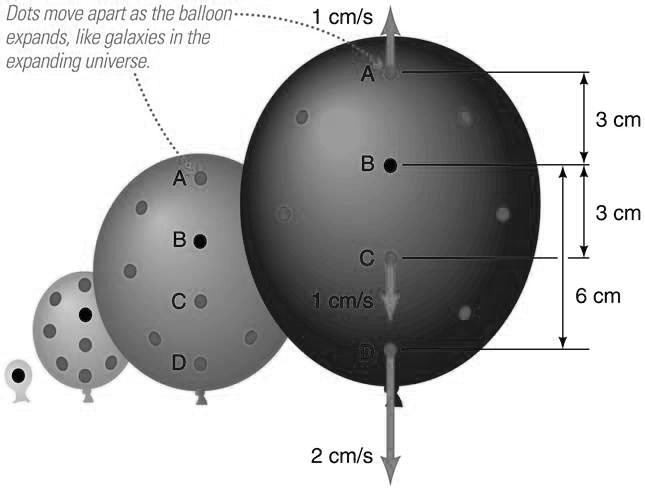
Watch how distance grows faster between farther dots. You're inflating your own Big Bang model!

Cosmic Candles — Measuring the Galaxies

Posted on June 10, 2025

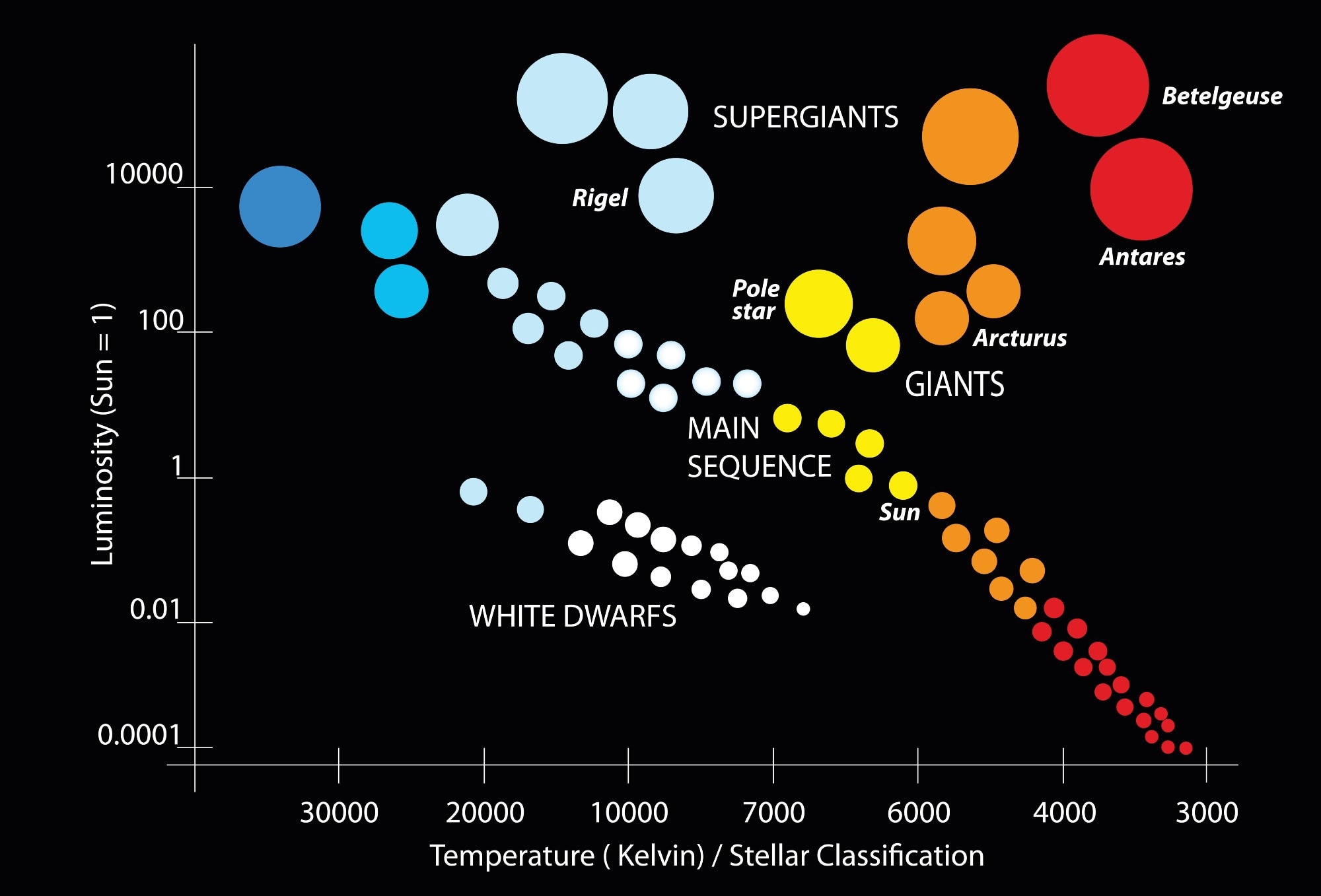
Parallax taps out at our galaxy's edge—too faint for farther. To map intergalactic voids, astronomers needed "standard candles": objects with known true brightness, like 100-watt bulbs anywhere. Spot one, gauge how dim it looks (fainter = farther), and boom—distance! Light dims with the square of distance (double away, quarter bright), so math reveals the gap. But finding reliable candles? That's where trailblazers like Henrietta Swan Leavitt shine.

The Brightness Trick

Imagine streetlights: Same bulb power, but the farthest looks tiniest. Stars work similarly, but vary wildly in "wattage" (luminosity). Solution: Pick ones with a secret code linking pulse to power. Enter Cepheids—pulsating stars that swell and shrink like breathing giants, brightening/dimming every 1-100 days. Brighter ones pulse slower; plot period vs. peak brightness, and you calibrate the candle.

The Cepheid Secret

Born in 1868, Henrietta was a "computer" at Harvard—women crunched data for male bosses, paid peanuts. In 1908, she cataloged blurry photos, spotting 1,777 variable stars in the Magellanic Clouds (our galaxy's satellite dwarfs). By 1912, studying 25 Cepheids there, she graphed: Longer blink = brighter intrinsic shine. "A simple relation," she wrote humbly, but it was revolutionary! All Cepheids at same distance (in the Clouds), so she nailed their yardstick. Edwin Hubble later used it on Andromeda, proving it's a separate galaxy 2.5 million light-years away—not a nebula.

Fun fact: Delta Cephei, the type's namesake, pulses 5.4 days. Leavitt discovered half the known variables then, despite no telescope time. Her period-luminosity law (now Leavitt's Law) scaled the universe to billions of light-years. Today, Hubble and James Webb scopes hunt Cepheids for cosmic tape measures.

By comparing true vs. apparent brightness, we mapped galaxy clusters. Cepheids lit the way from Milky Way to mega-structures!

Activity: Light Layers

1. Grab a bright bulb or phone flashlight in a dark room.
2. Measure its "brightness" (wall glow) at 1 meter.
3. Add tissue layers or move farther; note dimming (inverse square law: distance x2, brightness /4).
4. Predict a "Cepheid" by timing flashlight blinks—longer "pulse" = "brighter" assumed power.

That’s how distance dims light—the same principle that built the galactic scale. You're now a cosmic surveyor!

Beyond the Sun — Measuring Stars

Posted on May 10, 2025

With the solar system mapped to scale, astronomers got ambitious: How far to the stars? Our Sun's just one pinprick in a sky of billions. Stars are so distant, light takes years (or millennia) to reach us. Enter parallax—the ultimate cosmic tape measure, using Earth's orbit as a baseline. It's like holding your thumb up and winking eye-to-eye; the thumb "jumps" against the background. For stars, Earth is the eyes, six months apart (300 million km baseline). The closer the star, the bigger the shift. But those shifts? Tinier than a pixel on your phone screen.

The Parallax Method

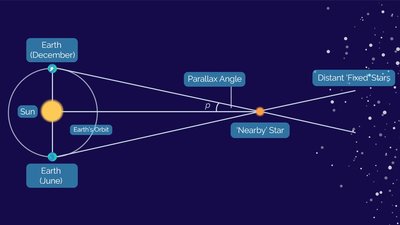
Ancient Greeks dreamed of parallax but couldn't spot it—stars seemed fixed. Galileo tried with his new telescope in 1610 but failed; tech wasn't sharp enough. By the 1800s, better scopes sparked a race. Enter Friedrich Bessel, a German math whiz born in 1784. Self-taught astronomer, he targeted 61 Cygni, a "flying star" that zipped across the sky. From 1837-1838, Bessel measured its position obsessively, calculating a parallax of 0.31 arcseconds (1/10,000th a degree—like spotting a firefly in New York from LA). That pegged it at 11 light-years away—first star distance ever! Fun fact: Bessel also predicted Neptune's existence and measured Sirius's wobble, hinting at an invisible "dark" companion (a white dwarf, confirmed later).

Parallax maxes at about 1,000 light-years; beyond, shifts are invisible. But it proved stars are suns like ours, scattered in a vast "Milky Way" disk. Today, ESA's Gaia satellite has mapped 2 billion stars' parallaxes, revealing our galaxy's 3D shape. Proxima Centauri, nearest at 4.2 light-years, shifts just 0.77 arcseconds—imagine measuring a coin's width on the Moon!

The First Success

Bessel's win in 1838 beat rivals like Thomas Henderson (who measured Alpha Centauri secretly in 1832 but published late). It shattered the idea of a small universe, showing stars are neighbors in a huge stellar city. Parallax isn't just history—it's how we hunt exoplanets and map cosmic neighborhoods.

Activity: Thumb Trick

1. Stretch your arm, thumb up, against a distant wall poster.
2. Close one eye, then the other—thumb "shifts" versus background.
3. Bring thumb closer; shift grows—like a nearby star!
4. Measure angles with a protractor for "parallax angle." Farther thumb = smaller angle, like dim stars.

That’s the same principle astronomers use to measure stars. Your hand just spanned light-years!

Locking the Scale — The Astronomical Unit

Posted on March 10, 2025

Kepler nailed the shapes of planetary orbits—squished ellipses, not circles—but he had no ruler for their size. Imagine drawing a map without knowing if the lines are miles or millimeters. Astronomers needed a "gold standard" distance: from Earth to the Sun, now called 1 Astronomical Unit (AU), about 150 million km. Locking this scale unlocked the solar system's true size. Enter epic sky events and clever timing that turned dreams into measurements.

The Transit of Venus

Every 105-121 years, Venus zips between Earth and Sun, appearing as a tiny black dot crawling across the Sun's face—like a bug on a lightbulb. It's called a transit, and it happens in pairs eight years apart. In 1716, comet-chasing genius Edmond Halley (of Halley's Comet fame) had a brainstorm: Watch the transit from different Earth spots, note slight timing differences, and use geometry like Eratosthenes did for Earth's size. The farther apart observers, the bigger the parallax shift, revealing the Sun's distance.

Halley died before the 1761 transit, but his idea sparked global teamwork. Kings funded expeditions—Captain Cook sailed to Tahiti for the 1769 show, dodging pirates and storms. Over 150 scientists worldwide timed Venus's 6-hour crawl with stopwatches and telescopes. Indian observatories in Madras joined in! Crunching the numbers (with some errors from Venus's fuzzy edges), they pegged 1 AU at about 153 million km—spot-on for the era. Fun fact: The next transit duo is in 2117 and 2125. Mark your calendars... or your great-great-grandkids'!

Measuring the Speed of Light

With 1 AU in hand, Danish astronomer Ole Rømer turned it into a speed gun for light in 1676. He timed eclipses of Jupiter's moon Io, which dips into Jupiter's shadow every 42 hours like clockwork. But when Earth was on the far side of its orbit (300 million km extra from Jupiter), eclipses lagged by 16-22 minutes. Rømer realized: Light takes time to travel! That delay covered twice 1 AU, so light zips 220,000 km/s—close to today's 300,000 km/s. Before Rømer, folks thought light was instant. He proved the universe has speed limits, kickstarting physics revolutions.

These feats showed science thrives on patience and collaboration. Today, radar bounces off Venus for pinpoint AU accuracy, but transits remind us: Rare events can measure the cosmos.

Activity: Torch and Coin Timing

You’ll need: A coin, a torch, a stopwatch.

Steps:

1. Shine the torch at a wall from 1 meter away.
2. Swiftly pass the coin through the beam to cast a moving shadow; time the crossing.
3. Double the distance (torch farther); time again—shadow moves slower!
4. Calculate "light delay" like Rømer: Longer path = longer time. Scale up to cosmic distances.

Even tiny timing differences can tell big distances! Who knew a coin could mimic Jupiter's moons?

Kepler’s Genius — Mapping the Solar System

Posted on February 10, 2025

Picture this: It's the early 1600s, and the night sky is a giant puzzle. People thought planets zipped around the Sun in perfect circles, like marbles on a track. But one determined guy, Johannes Kepler, spent years crunching numbers and staring at stars to crack the code. Born in 1571 in Germany, Kepler was a skinny kid with bad eyesight and a love for math. He dreamed of becoming a pastor but got hooked on astronomy after seeing a comet streak across the sky as a teen. Fast forward to 1600, and he's assisting the famous (and kinda quirky) astronomer Tycho Brahe.

Tycho was a Danish nobleman with a golden nose—literally! He lost part of his real nose in a duel and wore a fancy replacement. Tycho built an island observatory called Uraniborg, like a cosmic castle, and spent 20 years tracking planets with super-precise tools (no telescopes yet). He measured Mars's position night after night, creating the best data ever. But Tycho believed Earth was the center of everything, not the Sun. When he died suddenly in 1601 (legend says from a burst bladder after holding his pee too long at a party), he left his mountain of notes to Kepler, his young assistant. Kepler called it his "treasure"—and it changed everything.

The Mars Trick

Kepler dove into Tycho's Mars data like a detective on a case. Mars is tricky because its orbit crosses Earth's, making it look like it's doing loop-de-loops in the sky (called retrograde motion). Kepler compared Mars's position every 687 days—that's one Mars year. Since Mars returns to the same spot, but Earth has lapped it, he could back-calculate Earth's position. It was like using Mars as a mirror to see our own orbit. After thousands of calculations (by hand—no computers!), Kepler realized circles didn't fit. He tried ovals, but only ellipses worked perfectly. Boom—Kepler's First Law: Planets orbit the Sun in ellipses, with the Sun at one focus, like an egg's stretched circle.

But wait, there's more! Kepler's Second Law says a planet sweeps equal areas in equal times. When close to the Sun, it speeds up—like a kid on a swing flying faster at the bottom. Farther out, it slows down. And his Third Law? The time a planet takes to orbit (its year) squared equals its average distance from the Sun cubed. Math magic that predicts orbits for all planets!

The Big Discovery

It took Kepler eight years of "painful math" (his words) to publish his laws in 1609 and 1619. These weren't just facts—they smashed the old Earth-centered model and backed Copernicus's Sun-centered one. Fun fact: Kepler was also an astrologer (stars influencing personalities) and wrote a sci-fi story about a trip to the Moon. His work paved the way for Newton to figure out gravity. Today, we use Kepler's laws for everything from satellite launches to exoplanet hunts. NASA's Kepler telescope (2009-2018) discovered over 2,600 worlds beyond our solar system!

Activity: Draw Elliptical Orbits

You’ll need: Paper, pencil, string, and two pins.

Steps:

1. Push two pins close together—these are the “foci.” (One's the Sun!)
2. Tie the string into a loop and loop it around both pins.
3. Keep the string taut with the pencil and draw around—you'll make an ellipse.
4. Try different pin distances or string lengths for squished or round orbits. Label planets and see how close ones are more oval.

That's how Kepler uncovered the solar system's true dance—elliptical, speedy, and totally awesome. Next time you look up, remember: the planets are grooving to his beat!

Earth, Moon, and the Sun’s Great Secret

Posted on November 10, 2025

Once Earth’s size was known, another Greek scientist, Aristarchus of Samos, looked up and asked,

“If I know how big Earth is, can I find how far the Moon and Sun are?”

Measuring the Moon’s Distance

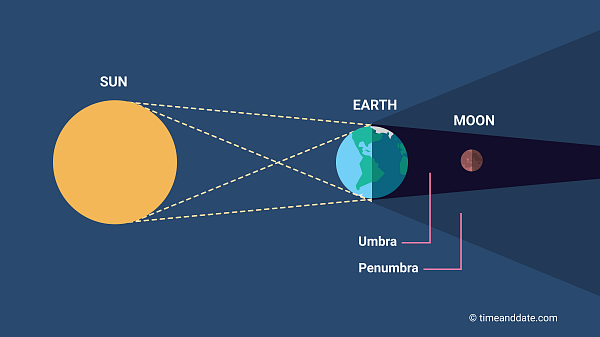
Aristarchus studied lunar eclipses — when Earth blocks sunlight and its round shadow falls on the Moon.

He noticed that Earth’s shadow looked about 2.5 times wider than the Moon itself.

He also timed how long the Moon took to pass through the shadow — about 3 hours.

Since the Moon takes 27 days to complete one orbit, he used geometry and ratios to compare how far it moved during those 3 hours versus its whole orbit.

Using the known size of Earth, he worked out that the Moon must be about 60 Earth radii away.

Modern value: 60.3 Earth radii. Amazing accuracy without telescopes!

Finding the Sun’s Distance

Next, Aristarchus turned to the half-moon phase.

When the Moon looks exactly half lit, the Sun, Earth, and Moon make a right triangle.

If he could measure the angle between the Sun and Moon, he could find how far away the Sun was.

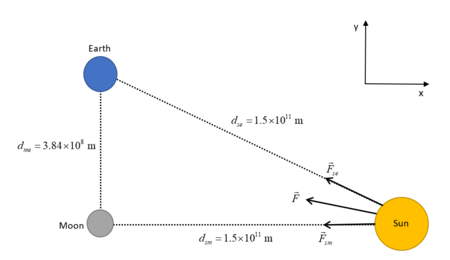
The trouble was that the angle was very small — less than 1°. His eyes weren’t precise enough.

He thought the Sun was 20 times farther than the Moon. In truth, it’s about 370 times!

Still, Aristarchus made a bold leap: since the Sun was so large, it must be the center and Earth must move around it.

That was the first heliocentric model — nearly 1,800 years before Copernicus!

Activity: Shadow and Coin Experiment

You’ll need:

• A coin
• A torch or candle
• A wall or screen
• A ruler

Steps:

1. Place the torch on a table, pointing at the wall.
2. Hold the coin in front of it to make a circular shadow.
3. Move the coin closer or farther and note how the shadow changes size.
4. Use a ruler to measure distances and shadow diameters.

You’ve just learned how light and shadow reveal distance — the same idea Aristarchus used to measure the heavens!

How Far Is Far? The Incredible Story of Measuring the Earth

Posted on September 10, 2025

Imagine standing outside on a sunny afternoon. You look at your shadow. Now imagine someone else, far away, doing the same thing — and their shadow is a little different!

Would you believe that this tiny difference helped a man 2,000 years ago measure the entire size of the Earth?

Let’s travel back to ancient Egypt, around 250 BC. A wise man named Eratosthenes worked in the great library of Alexandria.

The Clue from a Deep Well

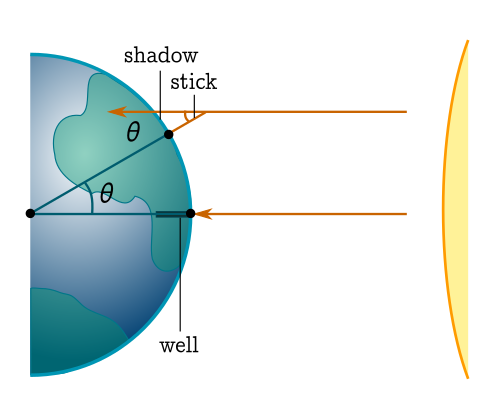
Eratosthenes had heard that in Syene (now Aswan), on the day of the summer solstice, the Sun stood straight overhead. Sunlight fell straight into a deep well — no shadow at all!

But in Alexandria, far to the north, a stick still made a small shadow at the same time.

He thought, “If sunlight falls at different angles, the Earth must be curved!”

Measuring with Shadows

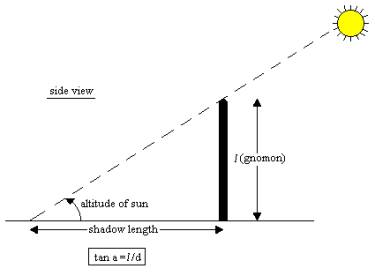
At noon on the solstice, he placed a stick (a gnomon) upright in the ground and measured the shadow.

The Sun’s rays were tilted by about 7.2°, which is 1/50th of a full circle (360°).

The distance between Alexandria and Syene was about 800 km.

So, if 7.2° equals 800 km, the whole circle (360°) must be:

360 × 800 ÷ 7.2 = 40,000 km.

That’s almost the real circumference of Earth — measured 2,000 years ago with only a stick and sunlight!

Activity: Measure Earth’s Diameter

You’ll need:

• A straight stick (1 m)
• A ruler and protractor
• A watch or phone clock
• A friend in another city
• Google Maps to measure distance

Steps:

1. On the same date and time (solar noon), fix your stick upright on flat ground.
2. Measure the length of its shadow.
3. Calculate the Sun’s angle: angle = arctan(shadow ÷ stick height).
4. Ask your friend to do the same.
5. Find the difference in the Sun’s angle between both places.
6. Use this formula: Earth’s circumference = 360 × distance ÷ angle difference.
7. Divide by π to get diameter.

स्वयंप्रकाशी तू तारा

Posted on August 5, 2024

सवाल:

जैवप्रदीपक जीव: निसर्गाचा प्रकाश चमत्कार

काय असेल याच ऊत्तर. कोणता असा प्रवासी असेळ जो दिवा पाठीलाच बांधून फिरतो. तर तो आहे सर्वपरिचित असलेला काजवा! हा छोटासा पण अत्यंत आश्चर्यकारक कीटक आपल्या शरीरातून प्रकाश निर्माण करतो. निसर्गात असे बरेच जीव आहेत जे असा दिवा घेऊन येतात जन्माला — जे स्वतः प्रकाश तयार करतात — जसे समुद्रातील प्लवक, काही मासे, शैवाल, आणि अगदी काही बुरशीदेखील यातल्या काही मोजक्याच प्राजाती चमकतात (सगळे चमकत असते तर रात्री जग काही वेगळंच दिसलं असतं). अशा जीवांना वैज्ञानिक भाषेत जैवप्रदीपक (Bioluminescent) जीव म्हणतात.

पण हे जीव का चमकतात? आणि तेही वेगवेगळ्या रंगांत का? चला, यामागचं विज्ञान आणि निसर्गाचं सौंदर्य समजून घेऊया.

का चमकतात हे जीव?

प्रकाश निर्माण करणं म्हणजे ऊर्जा खर्च करणं. मग अशा प्रक्रियेचा उपयोग काय? यामागे अनेक जैविक कारणं आहेत.

• संवादासाठी – काजवे आपल्या जोडीदारांना आकर्षित करण्यासाठी चमकतात. प्रत्येक प्रजातीचा प्रकाशाचा पॅटर्न वेगळा असतो. काही झपाट्याने चमकतात, काही हळूहळू — त्यामुळे काजव्यांना एकमेकांना ओळखणं सोपं जातं.
• संरक्षणासाठी – काही जीव चमकून आपल्या शत्रूला गोंधळात टाकतात. उदाहरणार्थ, काही प्लवक प्रजाती चमकून पाण्यात झळाळी निर्माण करतात, ज्यामुळे शिकारी मासे घाबरून दूर जातात.
• शिकार करण्यासाठी – खोल समुद्रातील अँगलर फिश आपल्या तोंडासमोर लटकवलेल्या दिव्यासारख्या अवयवाने इतर माशांना आकर्षित करतो. एकदा शिकार जवळ आली की ती त्याच्या तोंडात गायब होते!
• अंधारात ओळखण्यासाठी किंवा मार्गदर्शनासाठी – समुद्राच्या तळाशी सूर्यप्रकाश पोहोचत नाही. तिथे राहणारे जीव स्वतःचा प्रकाश वापरून एकमेकांना पाहतात आणि मार्ग शोधतात.

हा प्रकाश तयार होतो कसा?

जैवप्रदीपनामागे एक सुंदर रासायनिक प्रक्रिया असते. या प्रक्रियेत ल्युसिफेरिन (Luciferin) नावाचं द्रव्य आणि ल्युसिफरेस (Luciferase) नावाचं एन्झाइम एकत्र येतात. ऑक्सिजनच्या उपस्थितीत दोघांमध्ये प्रतिक्रिया होते आणि त्यातून प्रकाश निर्माण होतो.

ही प्रक्रिया विलक्षण कार्यक्षम आहे — कारण यातून उष्णता जवळजवळ तयार होत नाही. म्हणजेच, जीव ‘थंड प्रकाश’ निर्माण करतात. म्हणूनच काजवा आपल्या शरीरातला प्रकाश उष्णतेशिवाय निर्माण करू शकतो.

सर्व जीव एकाच ल्युसिफेरिनचा वापर करतात का?

नाही. हेच या प्रक्रियेचं विशेष आहे. प्रत्येक प्रजातीचं ल्युसिफेरिन आणि ल्युसिफरेस थोडं वेगळं असतं. म्हणूनच त्यांच्या प्रकाशाचे रंग आणि तीव्रता वेगवेगळी असते.

• काजवे सहसा पिवळसर-हिरवा प्रकाश निर्माण करतात.
• समुद्री प्लवक निळसर प्रकाश देतात — कारण निळा रंग पाण्यात सर्वात लांब पसरतो.
• बुरशी हलका हिरवट प्रकाश देते, जो रात्रीच्या अंधारात मऊ आणि रहस्यमय वाटतो.
• काही खोल समुद्रातील मासे लाल किंवा केशरी प्रकाशही निर्माण करतात, कारण त्या लहरी दूरवर त्यांच्या शिकाऱ्यांना दिसत नाही, पण त्यांना मात्र इतर दिसतात.

अशा वेगळ्या रंगांमागे त्या जीवांचा परिसर, जीवनशैली आणि गरज यांचा थेट संबंध असतो. उदाहरणार्थ, समुद्रात निळा प्रकाश सर्वाधिक परिणामकारक ठरतो, तर जमिनीवर हिरवट-पिवळा प्रकाश डोळ्यांना जास्त दिसतो.

विज्ञानात आणि मानवजातीसाठी उपयोग

जैवप्रदीपनाचं निरीक्षण केवळ रोचक नाही, तर उपयोगीही ठरलं आहे. वैज्ञानिकांनी ल्युसिफेरिन आणि ल्युसिफरेस वापरून वैद्यकीय संशोधन, जनुक चाचण्या, आणि रासायनिक प्रयोग करायला सुरुवात केली आहे. प्रयोगशाळेत एखाद्या पेशीने विशिष्ट प्रतिक्रिया दिली की ती चमकू लागते — त्यामुळे वैज्ञानिकांना परिणाम दिसतात, जणू अंधारात ज्ञानाचा दिवा पेटतो.

निसर्गाचं अद्भुत सौंदर्य

आपण काजव्यांचा प्रकाश बघतो तेव्हा वाटतं जणू पृथ्वीवर तारे उतरले आहेत. पण जर आपण समुद्राच्या खोल भागात जाऊ शकलो, तर तिथलं जग आणखीच जादुई आहे — निळ्या, हिरव्या, आणि लाल रंगांच्या झगमगाटात निसर्गानं रंगवलेलं एक परीकथेसारखं दृश्य.

हे जीव आपल्याला शिकवतात की प्रकाश बाहेरून नाही, आतून निर्माण होऊ शकतो. काही वेळा अंधार असलाच पाहिजे — तेव्हाच आपल्या आतल्या प्रकाशाचं सौंदर्य खऱ्या अर्थानं दिसतं.

अशा या काजव्यांपासून समुद्रातील चमकणाऱ्या जीवांपर्यंत सगळ्यांच्या कहाणीत एक समान धागा आहे — जगण्यासाठी, संवादासाठी आणि सौंदर्यासाठी प्रकाश हा निसर्गाचा स्वतःचा चमत्कार आहे.

Plastic Mulch, a bad choice?

Posted on September 15, 2022

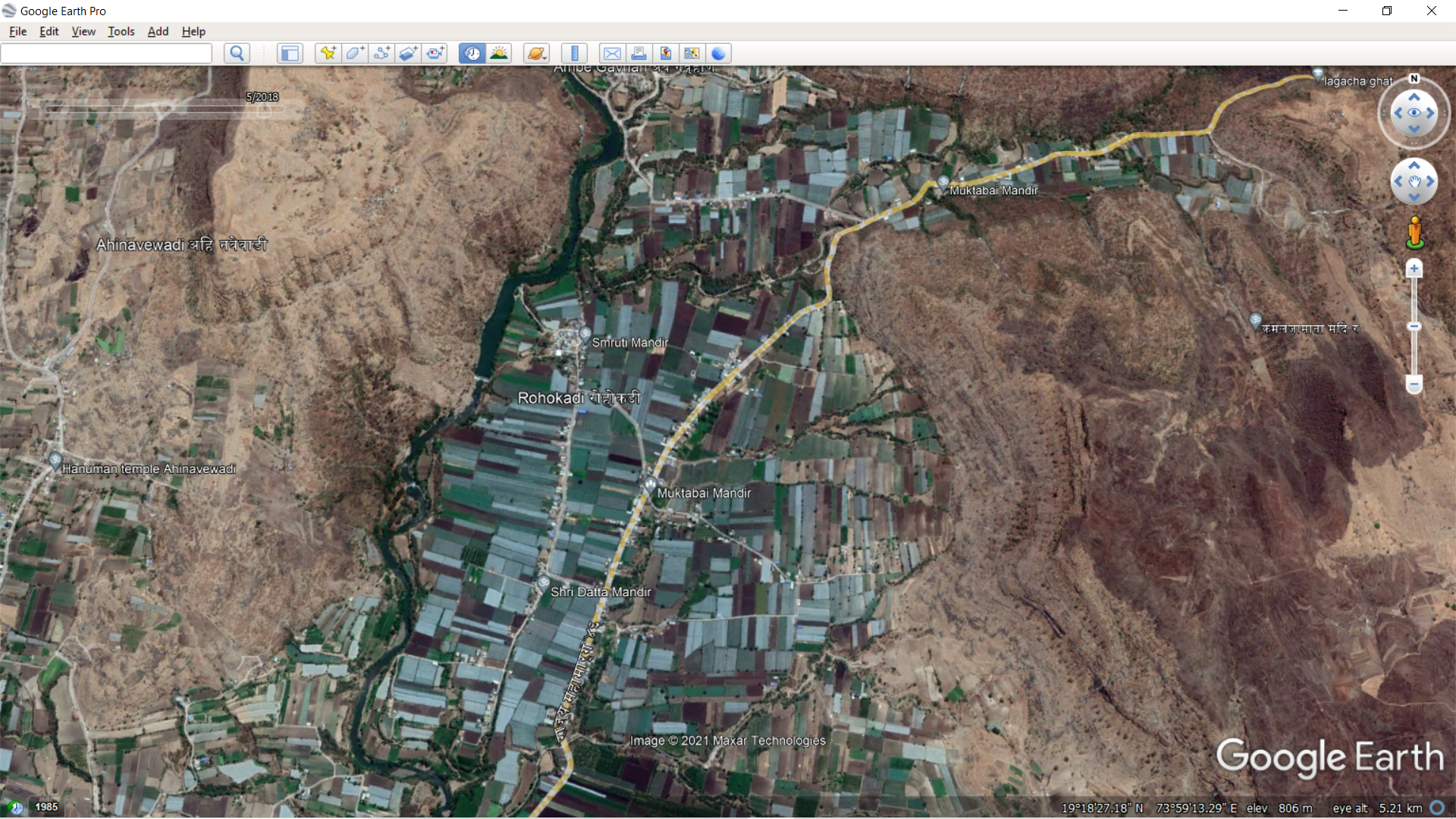
I was looking at old Google Earth images of my village and found one from 2018. The white areas in the fields are plastic mulch, which we farmers use to increase crop yields. But another picture shows our problem with getting rid of this plastic. The mulch is a 25-micron plastic film, and each acre needs 5-6 bundles, each weighing about 10 kg. If you search for my village, Rohokadi, and the surrounding area in the historical data, you’ll see the issue farmers might face soon. While plastic mulch has helped us grow better crops for the past 8-10 years, we are starting to notice some problems. Even though the mulch can be used for three crops in a row, most farmers only use it once and then throw it away. Over time, this plastic stops air from getting into the soil, which can harm the microbes that keep the soil healthy. This might make the soil less productive and lead to using more fertilizers.

Since mulch helps reduce water usage and weeds, it’s important for us to keep using it, especially in a developing country like ours. However, I’m concerned about the plastic waste it creates, so I’m looking for solutions. I’ve thought of a few ideas, and I’d love to collaborate if you have any thoughts on how they could be implemented:

1. Natural Foliage Mulch: Although using natural foliage as mulch is effective, collecting and spreading it can be difficult. I’m thinking about collecting this material and turning it into sheets that can be easily laid in the field.

2. Biodegradable Paper Mulch: Another idea is to coat craft paper with vegetable oil and cure it to make it into a water-resistant, degradable polymer. This paper could then be used as mulch.

A Thought-Provoking Start: Exploring "What is a Computer?" with Young Minds

Posted on January 30, 2022

The first day of teaching at Z. P. Primary School was an exciting one. I had planned to start with the CM1 module of the curriculum. Since attendance was low in the 7th class, I decided to introduce concepts gradually to avoid repeating lessons for absent students.

As I began the session with the question, "What is a computer?", I expected either silence or vague responses. However, one girl confidently answered, "A computer is an electronic device that takes input and gives output." Her precise definition surprised me and altered the direction of my lesson. My new challenge was to help her and the other students truly understand what the definition meant.

According to my lesson plan, I aimed to cover four key aspects:

• A computer is an electronic device.
• It works with information (input and output).
• It helps solve problems.
• It exists in various forms beyond office settings.

The class engaged actively in discussions, and most students grasped the fundamental concept of a computer. To reinforce their understanding, I posed a question: "Is a digital weighing machine a computer?" After a brief discussion, most students agreed that it utilizes a computer to function. This marked a good stopping point for the day.

During the discussion, I emphasized that a computer processes information, handles input and output, and aids in problem-solving. Later, after interacting with her classmates, the same girl returned with a compelling question: "Is a human a computer?" She argued that humans also process information, take input and give output, and solve problems. Her curiosity sparked further debate, and I encouraged the class to think it over.

On another day, when the absent students returned, she eagerly steered the session back to her question. We spent half an hour debating whether humans could be considered computers. Some students argued that computers cannot move, so I showed them a video of Boston Dynamics robots dancing. Others said that humans do not run on electricity, so I asked them to consider energy in broader terms—just as computers use electrical energy, humans derive energy from food.

One student finally noted a crucial distinction: "We have will and desire, but computers don’t." That moment became a natural pause in the discussion, and we returned to our planned lesson.

Even now, the question remains open for them to explore. Apart from will and desire, the students continue searching for more differences between humans and computers. This unplanned philosophical inquiry turned out to be an enriching experience, highlighting how curiosity can drive deep learning.

Teaching is not just about delivering content—it is about encouraging students to think, question, and seek answers beyond the obvious. And sometimes, the best lessons come from the questions we never expected.

Can you find the penumbral shadow?

Posted on January 02, 2020

I captured a video using a mobile phone and an 8-inch telescope of a partial penumbral lunar eclipse.

Don't be discouraged if you can't see the shadow. I might not have captured it perfectly. However, you will notice that the moon appears to rotate in the video. You might wonder, does the moon rotate like that? The short answer is no. In reality, the moon wobbles a little but doesn't rotate as seen in the video. The rotation in the video is due to the type of telescope mount we used—a Dobsonian mount. When the object we're observing passes the zenith (the point directly overhead), we have to adjust our viewing direction. This adjustment causes the frame of our recording device, which is attached to the telescope, to rotate.

Kno your weather

Posted on January 02, 2019

Here's a presentation I made for my class on atmospheric science, which I studied during my master's program. I chose this topic because I enjoy photographing and observing different types of clouds. Clouds can reveal important clues for predicting the weather. Additionally, I'm interested in folktales related to clouds. If you know of any, please let me know!

Measuring the impossibles

Posted on August 02, 2018

Here's a presentation I created for my class on the history of astronomical measurements, starting with basic observations and assumptions.